Aim: 

To determine the radius of curvature of a given spherical surface by a Spherometer. 

Apparatus: 

1. Spherometer
2. Glass Slab
3. Half Meter Scale
4. Convex Lens

Theory: 

A spherometer is a measuring instrument used to measure the radius of curvature of a spherical surface and a very small thickness. 

Figure 3.1 is a schematic diagram of a single disk spherometer. It consists of a central leg OS, which can be raised or lowered through a threaded hole V (nut) at the centre of the frame F. The metallic triangular frame F supported on three legs of equal length A, B and C. The lower tips of the legs form three corners of an equilateral triangle ABC and lie on the periphery of a base circle of known radius, r. The lower tip of the central screw, when lowered to the plane (formed by the tips of legs A, B and C) touches the centre of triangle ABC. A circular scale (disc) D is attached to the screw.  The circular scale may have 50 or 100 divisions engraved on it. A vertical scale P marked in millimetres or half-millimetres, called main scale or pitch scale P is also fixed parallel to the central screw, at one end of the frame F. This scale is kept very close to the rim of disc D but it does not touch the disc D. This scale reads the vertical distance when the central leg moves through the hole V.   

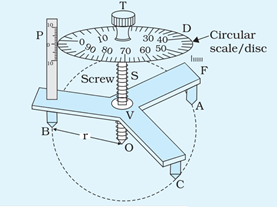
Fig 3.1      

Principle: 

Pitch of a Spherometer 

            The vertical distance moved by the screw S in one complete rotation of the circular Scale/Disc D is called the pitch (p) of the spherometer. To find the pitch, give full rotation to the screw (say 4 times) and note the distance (d) advanced over the pitch scale. 

If the distance d is 4 mm The pitch can be represented as, 

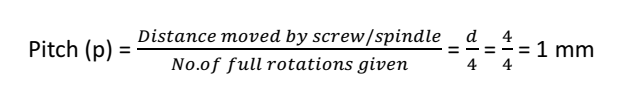
Least Count of the Screw Gauge 

The Least count (LC) is the distance moved by the spherometer screw, when the screw is turned through 1 division on the circular. We are using a spherometer which has 100 divisions (N) on the disc. The least count can be calculated using the formula, 

The formula for the radius of curvature of a spherical surface 

Approach 1: 

From the figure 3.3, O is the centre of the circle. OE = OA = R, radius of the circle. F is the tip of the screw at the same plane with A, B and C. EF = h, AF = a and ∠AFO =  

900. 

Therefore, geometrically we can write, 

OA2 = OF2 + FA2 

or, R2    = (R-h)2 + a2 

= R2 -2.R.h + h2 + a2 

∴ R = (h2 + a2 )/2h 

Now, let l be the distance between any two legs of the spherometer as shown in figure 3.6, then from geometry we have, a = . Thus the radius of curvature of the spherical surface can be given by, 

               ∴ R = ( 3h2 + l2 )/6h        

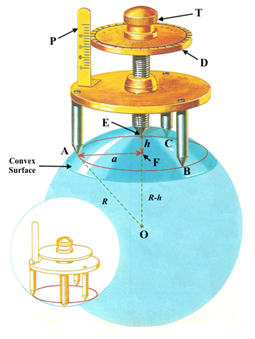
Fig 3.3 

Approach 2: 

From the figure 3.4, the circle is passing through A and C.  O is the centre of the circle. OE =R, radius of the circle. F is the tip of the screw at the same plane with A, B and C. CF = h, AF = a ∠EAC = 900. 

∴ CE2 = AE2 + AC2 

or, (2R2) = (AF2 + FE2) + (CF2 + AF2) 

                  = a2 + (2R -h)2 + h2 + a2 

∴ R=  a2/2h+ h/2 

Now, let l be the distance between any two legs of the spherometer or the side of the equilateral triangle ABC (Fig. 3.4), then from geometry we have, a = l/√3. Thus the radius of curvature of the spherical surface can be given by, 

R =  a2/2h+ h/2 

or, R = l2/6h+ h/2 

Diagram:  

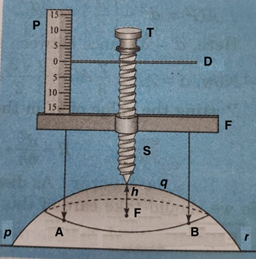
Fig 3.4 

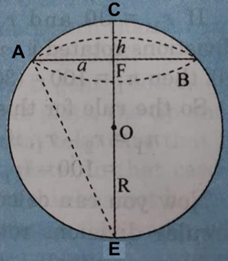
Fig 3.5 

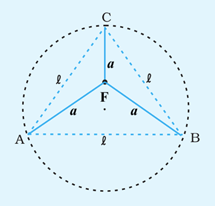
Fig. 3.6 

Procedure: 

1. Find the pitch (p) of the screw and count the total number of divisions (N) in the circular scale.
2. Place the spherometer in the plane glass plate. Now rotate the head T anti-clockwise to raise the tip of the central screw S by a certain distance.
3. Place the spherometer on the convex surface. Gently rotate T clockwise to bring down the tip of S until it just touches the spherical surface. Use a paper strip and try to pass between the tip of the screw and spherical surface to check if there is no gap between them.
4. Record the initial circular scale reading (r1) in table 3.1. Circular scale reading means the divisions engraved on the disc which coincides with the linear scale.
5. Place the spherometer on the glass slab without disturbing the initial circular scale reading (c.s.r). Then slowly rotate T clockwise to bring the tip down and touch the glass plate. During this rotation count the number of full rotation (n) of the circular scale. Take the final c.s.r. (r2) when the tip touches the glass plate.
6. Repeat step 2 and 5 at least thrice by placing the spherometer at different places.
7. Now, place the spherometer on a piece of paper and press it lightly so that an imprint of the three legs is made on the paper. You can do it on your laboratory notebook on the left side white page.
8. Measure each side of the triangle AB, BC, and CA formed by the points  (A, B, C).
9. Take mean of them. Thus we get l.

Observations: 

Least count of spherometer : 

Total number of divisions is the in circular scale, N = _______ 

One linear scale division, L.S.D.  = ____ mm 

Distance moved by the screw for 4 rotations, d = ________ mm 

Pitch of the screw, p = 4/d = ____mm 

Therefore, Least Count, L.C. = p/N= ______________mm 

Distance between two legs of spherometer: 

               AB = _______ cm, BC = _______cm, CA = _________cm 

∴ l = (AB + BC+ CA)/3 = _______________________cm 

Table 3.1 Table for height (h) 

Mean value of sagitta, h = _________________ mm = ________________cm 

Calculation: 

Radius of curvature of the given convex surface, R = (3h2 + l2 )/6h =…………………………..cm 

or, Radius of curvature of the given convex surface, R = l2/6h+ h/2 =…………………………… cm 

Precautions: 

1. The screw should move freely without friction.
2. The screw should be rotated in one direction to get any reading. Otherwise back-lash error will be introduced.
3. The circular should not be rotated any more, even slightly, when it touches a surface.
4. The linear scale is not used to take readings and h is calculated by taking the difference of two circular scale readings. Hence we do not need to find the zero error of the instrument.

Reference: 

1. http://www.ncert.nic.in/

Your may checkout our blog on  SCREW GAUGE & LEAST COUNT   

About Labkafe: Lab Equipment Manufacturer & Exporter

We are a School laboratory furniture and Lab equipment manufacturer and supplier. In laboratory furniture for school, we first design the entire laboratory room keeping in mind the requirements as per affiliation CBSE Bye-Laws. Also, we take care of the complete designing and installation of laboratory furniture. 

In the lab equipment section, we have a wide range of glassware, chemicals, equipment and other lab accessories. Most of them are available for order online on our website but some of them can be procured on demand. 

If you have need:- 

•       laboratory equipment or lab furniture requirements for school
•         composite lab equipment list for school
•         Physics lab equipment list for school
•         Chemistry lab equipment list for
•         Biology lab equipment list for school
•         Pharmacy lab equipment

do drop a message through chat or mail us at  sa***@la*****.com   or call +919007218364 and we’ll get in touch with you.